擬似相関と相関関係の違い
2016/11/24

混乱する人がけっこうといると思われる「擬似相関」と普通の「相関関係」の違いについて。
相関関係について
まず相関関係の説明から。
統計学基礎の王道書として有名な東大編集の統計学入門 (基礎統計学)、通称赤本の説明を紹介する。
二つの変数間の関係のことを、一般に相関関係と呼ぶが、とくに統計学では二つの変数の間に直線関係に近い傾向が見られるときに「相関関係がある」ということが多い。
一方の変数の増加につれて他方の変数も増加する場合を「正の相関関係がある」といい、逆に一方の変数の増加が他方の変数の現象と対応している場合を、「負の相関がある」という。直線的な傾向の程度は「強い」「弱い」と表現する。
引用元:統計学入門 (基礎統計学) 東京大学教養学部統計学教室編集 45p
相関関係と因果関係は異なる。たとえば身長と体重の間には相関関係があるが、どちらがどちらを決めるともいえないので因果関係とはいえない。数学の成績と理科の成績などもその例である。これに対して、先の人口と商店数の例などは、人口が商店数を決めていると考えられるので相関関係があると同時に因果関係がある。一方、相関関係とは二つのデータ間の直線的な関係のことであるが、因果関係には直線というような単純な関係ではなく、はるかに複雑な関係も含まれる。したがって、因果関係であっても相関関係にはなく、相関係数の値も低くなるものもある。たとえば極端な例として、xが与えられたときy=(x-8)^2として決まる場合を考えてみよう。データの大きさをn=15とし、(1,(1-8)^2),(2,(2-8)^2),…(15,(15-8)^2)という(xi,yi)を考えてみると、相関係数rxyは0となる。社会現象の分析では、相関関係と因果関係のみきわめが難しいものが多いが、とくに現象のモデルづくりの際にはこの区別が重要である。
引用元:統計学入門 (基礎統計学) 東京大学教養学部統計学教室編集 51,52p
これ以上削るところがないように思えるが、あえてざっくりまとめると
相関関係:一方が増減すると他方も増減するという関係性のみを示している。
例)数学の点数が高い人は理科の点数も高くて、数学の点数が低い人は理科の点数も低い傾向にある。
因果関係:一方がもう一方を決めている関係。逆は起こらない。
例)お金持ちほどフェラーリを持つ可能性が高くなるが、フェラーリを持ったからといってお金持ちになる可能性が高くなるわけではない。
こういう感じになるだろうか。
擬似相関について
対して、擬似相関(読み:ぎじそうかん)。
これは偽相関(読み:ぎそうかん)と呼ばれたり、見かけ上の相関と呼ばれたりもする。
そして呼び方が統一されていないことが暗喩しているように実は定義もあやふやになっていたりもする。(学的な場を除く)
様々ある定義を一からここで解説することはしないが、意味としては
2つの事象に因果関係がないのに、見えない要因(潜伏変数)によって因果関係があるかのように推測されること。擬似相関は、客観的に精査するとそれが妥当でないときにも、2つの集団間に意味の有る関係があるような印象を与える。
引用元:擬似相関 – Wikipedia
というのが最も代表的なものだと思う。
相関関係と擬似相関の違い
ここで多くの人が頭を抱える。
そもそも相関関係というのは因果関係の有無については言及していない。さきほども説明したように2変数の増減関係について言及しているだけだからだ。
つまり因果関係がなくても、その2変数の増減に直線的な関係性が見出される場合は「相関関係がある」と言える。
これでは「相関関係がある」と言える場合、同様に「擬似相関がある」と言えてしまうのではないだろうか?
つまり相関関係=擬似相関となってしまっているではないか、全く同じものなのではないだろうか?
そう思ってしまうのも無理はない。
まとめ記事では文脈に依存するだけ、本質的な違いはないというような説明もよく見かける。
が、これは間違いである。
(非常に分かりにくいが)両者は厳密には別物だ。
擬似相関というのは、2変数の相関を生み出している第三の原因変数が明らかになって初めて言及できるものである。
2つの(確率)変数間の擬似相関は、第三の原因変数を導入することで生み出される。
換言すれば、A と B の間の相関を見出す。従って、考えられる関係としては次の3つがある。A が B を発生させる
B が A を発生させる
または
C が A と B を発生させる最後の関係が擬似相関である。
引用元:擬似相関 – Wikipedia
これだけだとイメージしにくいと思うので、赤本のなかで擬似相関(ここではみかけ上の相関という呼び方になっている)について説明している箇所を紹介したい。
図3.12を見てほしい。きわめて強い正の相関関係が認められる。これは東京都23区について、xに飲食店の数をとり、yに金融機関の店舗数をとって、各区をプロットした散布図である。図からは、飲食店の多いところには金融機関も多いということになる。相関係数も、rxy=0.892と非常に高い。しかし、常識的に考えると、両者の間には直接的な関係はなく、レストランが多いからといって銀行が立地するわけでもないし、逆に銀行が多いからといってレストランが立地するわけでもない。
実はこの二つの変数は、人口、とくに居住者の人口である夜間人口ではなく、昼間人口という第3の変数を間にはさんで、強い正の相関関係が観察されるのである。
飲食店の数xも金融機関の店鋪数yも、潜在的な顧客の数をもとに立地が決まっていると考えるのが妥当だろう。実際、昼間人口zと飲食店数xと金融機関店舗数yについて散布図を描いてみると、それぞれ図3.13,3.14のようになり、明らかに両方とも強い正の相関関係が観察される(相関係数はrzx=0.835とrzy=0.815)。したがって、この三者の関係を図示すれば図3.15のようになる。このとき、昼間人口をはさんで、飲食店数と金融機関店舗数の間には相関関係が生じるが、このような相関関係はみかけ上の相関と呼ばれる。みかけ上の相関は容易に人の判断を誤らせることがある。
飲食店数と金融機関店舗数の間の相関係数はrxy=0.892であるが、見かけ上の相関であるので、値にはあまり意味がない。
引用元:統計学入門 (基礎統計学) 東京大学教養学部統計学教室編集 54p
この例でいえば
飲食店数xと金融機関店舗数yの2変数の変動に関わっている原因である昼間人口zという第三の関数が導入されて初めて、「擬似相関(見かけ上の相関)である」と言える。
この第三の要因がない状態では「擬似相関である」とは言えない。しかし「相関関係がある」とは言える。
非常に分かりにくいところではあるが、なるべく分かりやすいように図にすると以下のような感じになるだろうか。
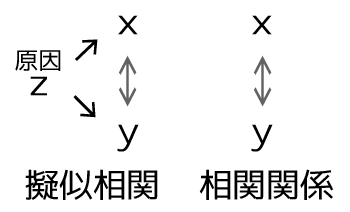
混乱しやすいし、同一視している情報も多々あるが実際にはこういった関係性の違いがある。
